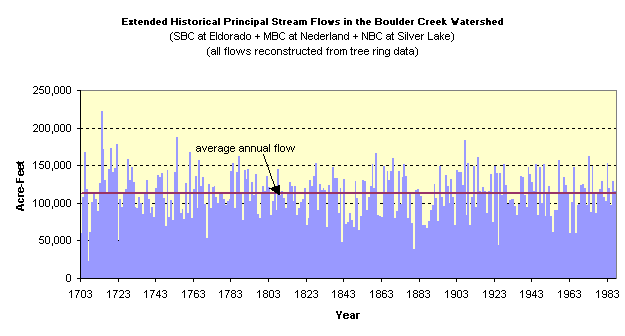
The above graph shows the combined natural flows of the Boulder Creek watershed's three principal streams - South Boulder Creek at Eldorado (SBC), Middle Boulder Creek at Nederland (MBC) and North Boulder Creek at Silver Lake (NBC) - over the period of 1703 through 1987.

These flows are based upon reconstructed flow data for MBC, derived from tree ring data by Dr. Connie A. Woodhouse (Institute of Arctic and Alpine Research, University of Colorado). The reconstructed MBC flow data were extended to the other two locations using correlation studies. This work was done by Hydrosphere as part of an ongoing project for the City of Boulder.

It should be noted that the graph shows only reconstructed flows and does not reflect actual recorded flows for the more recent period of recorded history (generally 1906 onward). This was done in order to illustrate the relative magnitude of low flow periods over the entire 285- year sequence in a correct manner. Thus, while the graph does not accurately depict actual flows during the 1953-1956 drought (they were lower than shown), it does accurately compare the relative severity of the 1950s drought to other droughts as evidenced by the tree ring data.

We can therefore confidently infer that the droughts of the 1840s and 1880s were more severe than that of the 1950s in terms of stream flow in the Boulder Creek watershed.

1. ¹ The reconstructed MBC flow data were extended to the other two locations by developing linear regression equations that quantified the correlations between recorded gage flows at MBC and calculated natural flows at the other two locations. Hydrosphere Resource Consultants had previously developed natural flow data for SBC and NBC. The correlations between annual flows at MBC and the two other locations are strong, explaining 83% of the variability at SBC and 91% of the variability at NBC. However, the correlations aren't perfect, so we added a random component to each of the regression equations that captures some of the uncertainty. The random component in each equation is equal to the standard deviation of the residuals for that equation times a normally distributed random number with mean of zero and standard deviation of one. This approach mimics the "error" seen in the regression equations and prevents all of the inflows from having perfect correspondence.

Return to Drought, Fire and Flood Homepage
Drought - Fire - Flood - It's All Connected